Linear Equations
Linear Equations are used to represent a straight line in mathematical terms.
x = 0 is a linear equation of one variable (x). It is represented on a graph as a dot.
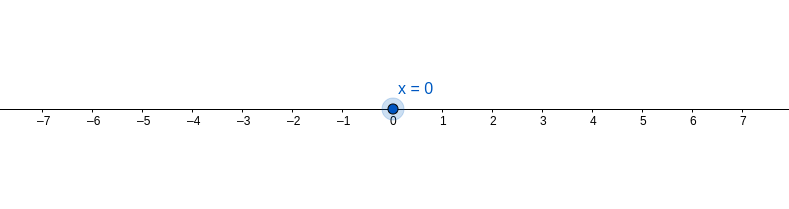
x = 0 could also be an equation of two variables (x and y).
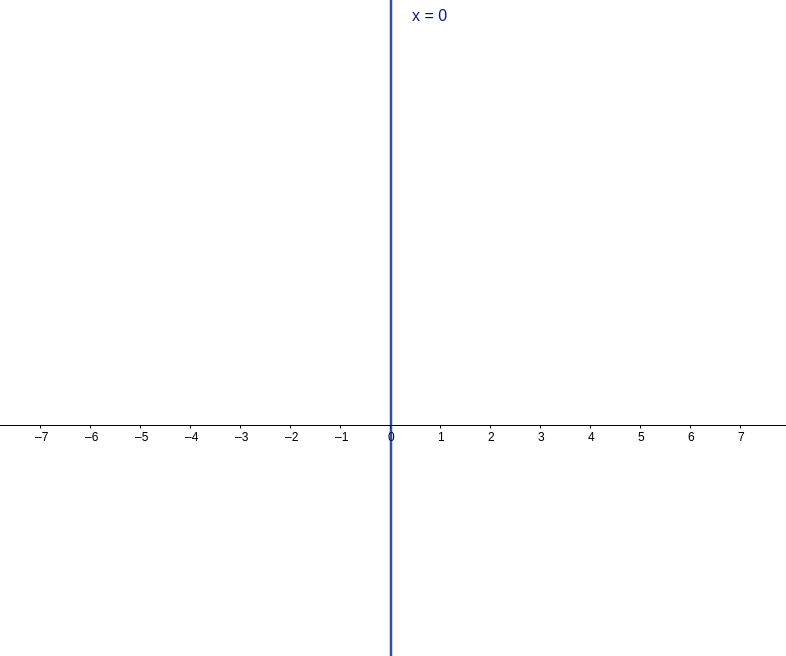
Like $ x - 0y = 0 $. In this equation, y can have any value but x will remain 0.
It is represented as a straight line along the y-axis.
2x + 3y = 6 is also an equation of two variables. It’s plotted on the graph below.
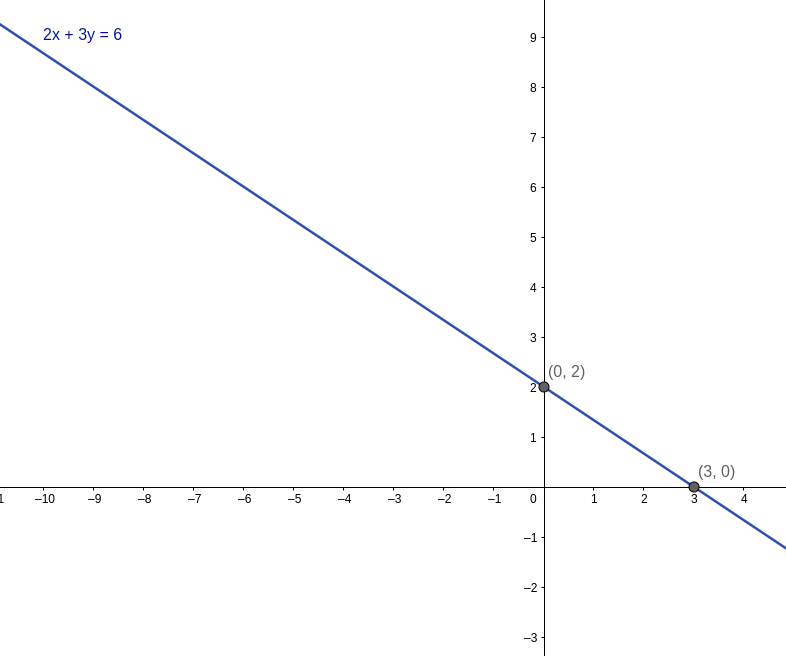
It intersects x-axis and y-axis at (0,2) and (3,0) respectively. So if we put those values inside the equation we get
-
Putting x = 0 and y = 2 in equations 2x + 3y = 6
\(2(0) + 3(2) = 6\)
\(0 + 6 = 6\)
\(6 = 6\) -
Putting x = 3 and y = 0 in equations 2x + 3y = 6
\(2(3) + 3(0) = 6\)
\(6 + 0 = 6\)
\(6 = 6\)
Hence, both of the points satisfy the equation. Though any point that’s on the line should satisfy the equation.
System of Linear Equations
If we model a problem into a set of linear equations that would be a system of linear equations.
There might be a common value of x and y such that it satisfies all the equations, that value will be called the solution of the system of linear equations.
Example
Suppose that the constraint of a problem is modeled using these equations.
\(x-2y = 6\)
\(x-y = 4\)
\(x+y = 0\)
Then the solution of this system of equations will be the values of x and y that satisfy all the constraints.
If we have to find the solution we can plot them on the graph and find the point common to all three lines.
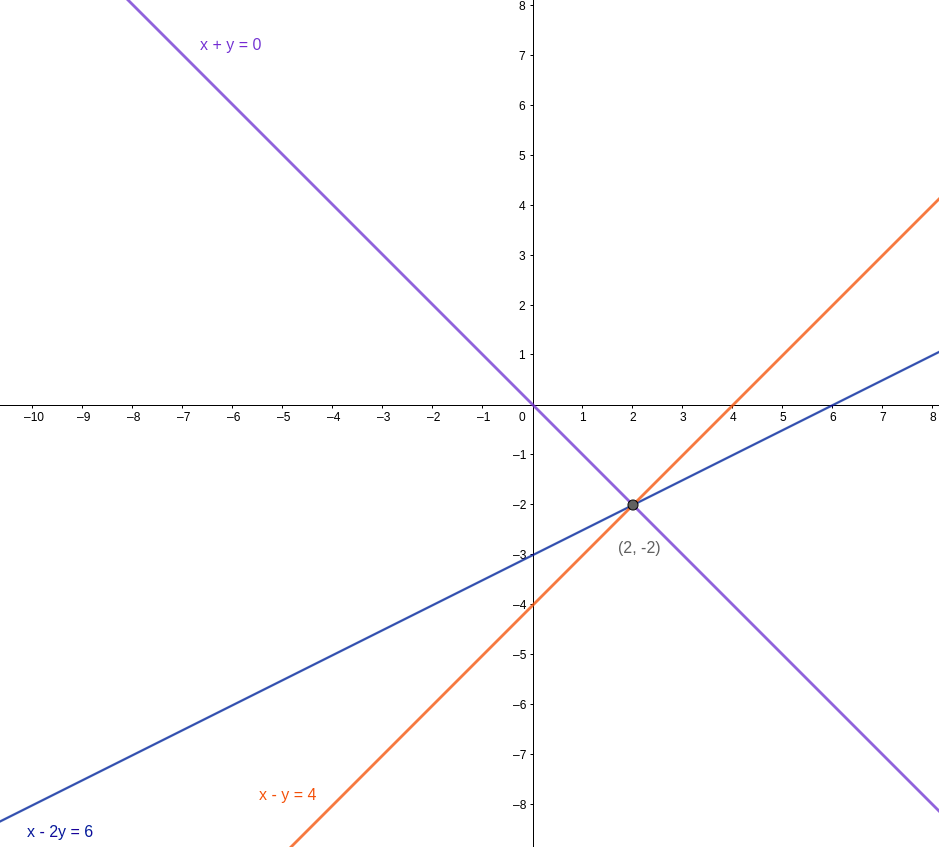
(2, -2) is the only point that satisfies all three equations so it is the solution. There are various methods of finding a solution to the system of linear equations. The one mentioned above is called the graphical method. The others are
- Substitution Method
- Elimination Method
Substitution Method
It has three steps
- Express one of the variables in terms of another variable.
- Convert any one equation of two variables into the equation of a single variable and find the value of that variable.
- Substitute the variable with its value in the equation and obtain the value of the second variable.
Example
We assign roman numerals to equations as (i), (ii) and (iii).
\(x-2y = 6\ \ \ \ \ \rightarrow (i)\)
\(x-y = 4\ \ \ \ \ \ \ \rightarrow (ii)\)
\(x+y = 0\ \ \ \ \ \ \ \rightarrow (iii)\)
Using (i) we will express variable x in terms of y.
\(x = 6 + 2y\)
This value of x will be substituted in (ii) to convert it to an equation of a single variable (y).
\((6 + 2y) - y = 4\)
\(6 + y = 4\)
\(y = (-2)\)
Now that we have value of the y we can substitute it in (iii).
\(x + (-2) = 0\)
\(x = 2\)
Indeed, (2, -2) is the solution of the system of linear equations (i), (ii) and (iii) as we saw in the graphical method previously.
Elimination method
The objective of this method is to find the value of any variable by eliminating all the other variables from the system.
- Multiply one of the equation with some constant.
- Perform addition or subtraction with another equation such that it eliminates all of the variables except one.
- Find the values by substitution.
Example
Multiply (ii) with 2
\(2(x-y) = 2(4)\)
\(2x - 2y = 8 \ \ \ \ \ \rightarrow (iv)\)
Subtract (iv) from (i)
\(x - 2y - (2x - 2y) = 6- 8\)
\(-x = -2\)
\(x = 2\)
Put x = 2 in (iii)
\(2 + y = 0\)
\(y = -2\)
The solution from the elimination method is also (2, -2).